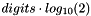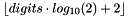A meta-template for querying various properties of fundamental types. More...
Static Public Member Functions | |
| static T | min () |
| The minimum finite value representable by the numeric type T. More... | |
| static T | lowest () |
The lowest finite value representable by the numeric type T, that is, a finite value 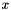 such that there is no other finite value such that there is no other finite value 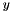 where where 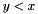 . More... . More... | |
| static T | max () |
| The maximum finite value representable by the numeric type T. More... | |
| static T | epsilon () |
The machine epsilon, that is, the difference between 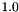 and the next value representable by the floating-point type T. More... and the next value representable by the floating-point type T. More... | |
| static T | round_error () |
The largest possible rounding error in ULPs (units in the last place) as defined by ISO 10967, which can vary from 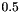 (rounding to the nearest digit) to (rounding to the nearest digit) to 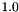 (rounding to zero or to infinity). More... (rounding to zero or to infinity). More... | |
| static T | infinity () |
| The special value positive infinity, as represented by the floating-point type T. More... | |
| static T | quiet_NaN () |
| The special value quiet not-a-number, as represented by the floating-point type T. More... | |
| static T | signaling_NaN () |
| The special value signaling not-a-number, as represented by the floating-point type T. More... | |
| static T | denorm_min () |
The minimum positive subnormal value of the type T, if OFnumeric_limits<T>::has_denorm != OFdenorm_absent, otherwise returns OFnumeric_limits<T>::min(). More... | |
Static Public Attributes | |
| static const OFBool | is_specialized |
OFTrue for all T for which there exists a specialization of OFnumeric_limits, OFFalse otherwise. More... | |
| static const OFBool | is_signed |
OFTrue for all signed arithmetic types T and More... | |
| static const OFBool | is_integer |
OFTrue for all integer arithmetic types T and OFFalse otherwise. More... | |
| static const OFBool | is_exact |
OFTrue for all arithmetic types T that use exact representation. More... | |
| static const OFBool | has_infinity |
OFTrue for all types T capable of representing the positive infinity as a distinct special value. More... | |
| static const OFBool | has_quiet_NaN |
OFTrue for all types T capable of representing the special value Quiet Not-A-Number. More... | |
| static const OFBool | has_signaling_NaN |
OFTrue for all types T capable of representing the special value Signaling Not-A-Number. More... | |
| static const OFfloat_denorm_style | has_denorm |
| Identifies the floating-point types that support subnormal values. More... | |
| static const OFBool | has_denorm_loss |
OFTrue for all floating-point types T capable of distinguishing loss of precision due to denormalization from other causes of inexact result. More... | |
| static const OFfloat_round_style | round_style |
| Identifies the rounding style used by the floating-point type T whenever a value that is not one of the exactly representable values of T is stored in an object of that type. More... | |
| static const OFBool | is_iec559 |
OFTrue for all floating-point types T which fulfill the requirements of IEC 559 (IEEE 754) standard. More... | |
| static const OFBool | is_bounded |
OFTrue for all arithmetic types T that represent a finite set of values. More... | |
| static const OFBool | is_modulo |
OFTrue for all arithmetic types T that handle overflows with modulo arithmetic, that is, if the result of addition, subtraction, multiplication, or division of this type would fall outside the range ![$[min(), max()]$](form_0.png) , the value returned by such operation differs from the expected value by a multiple of , the value returned by such operation differs from the expected value by a multiple of 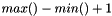 . More... . More... | |
| static const int | digits |
| The number of digits in base-radix that can be represented by the type T without change. More... | |
| static const int | digits10 |
| The number of base-10 digits that can be represented by the type T without change, that is, any number with this many decimal digits can be converted to a value of type T and back to decimal form, without change due to rounding or overflow. More... | |
| static const int | max_digits10 |
| The number of base-10 digits that are necessary to uniquely represent all distinct values of the type T, such as necessary for serialization/deserialization to text. More... | |
| static const int | radix |
| The base of the number system used in the representation of the type. More... | |
| static const int | min_exponent |
The lowest negative number 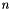 such that such that 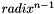 is a valid normalized value of the floating-point type T. More... is a valid normalized value of the floating-point type T. More... | |
| static const int | min_exponent10 |
The lowest negative number 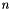 such that such that 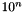 is a valid normalized value of the floating-point type T. More... is a valid normalized value of the floating-point type T. More... | |
| static const int | max_exponent |
The largest positive number 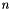 such that such that 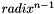 is a valid normalized value of the floating-point type T. More... is a valid normalized value of the floating-point type T. More... | |
| static const int | max_exponent10 |
The largest positive number 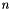 such that such that 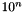 is a valid normalized value of the floating-point type T. More... is a valid normalized value of the floating-point type T. More... | |
| static const OFBool | traps |
OFTrue for all arithmetic types T that have at least one value that, if used as an argument to an arithmetic operation, will generate a trap. More... | |
| static const OFBool | tinyness_before |
OFTrue for all floating-point types T that test results of floating-point expressions for underflow before rounding. More... | |
Detailed Description
template<typename T>
struct OFnumeric_limits< T >
A meta-template for querying various properties of fundamental types.
The template OFnumeric_limits provides a standardized way to query various properties of fundamental types (e.g. the largest possible value for type int is OFnumeric_limits<int>::max()). OFnumeric_limits is compatible to C++11's std::numeric_limits.
- Template Parameters
-
T The type to inspect.
Member Function Documentation
◆ denorm_min()
|
static |
The minimum positive subnormal value of the type T, if OFnumeric_limits<T>::has_denorm != OFdenorm_absent, otherwise returns OFnumeric_limits<T>::min().
- Note
- Only meaningful for floating-point types.
C++11 standard definitions used:
| T | denorm_min() |
|---|---|
| non-specialized | T() |
| OFBool | OFFalse |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | usually 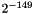 |
| double | usually 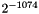 |
◆ epsilon()
|
static |
The machine epsilon, that is, the difference between 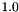 and the next value representable by the floating-point type T.
and the next value representable by the floating-point type T.
- Note
- It is only meaningful if
OFnumeric_limits<T>::is_integer == OFFalse.
C++11 standard definitions used:
| T | epsilon() |
|---|---|
| non-specialized | T() |
| OFBool | OFFalse |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | FLT_EPSILON |
| double | DBL_EPSILON |
◆ infinity()
|
static |
The special value positive infinity, as represented by the floating-point type T.
- Note
- Only meaningful if
OFnumeric_limits<T>::has_infinity == OFTrue. - In IEEE 754, the most common binary representation of floating-point numbers, the positive infinity is the value with all bits of the exponent set and all bits of the fraction cleared.
C++11 standard definitions used:
| T | infinity() |
|---|---|
| non-specialized | T() |
| OFBool | OFFalse |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | HUGE_VALF |
| double | HUGE_VAL |
◆ lowest()
|
static |
The lowest finite value representable by the numeric type T, that is, a finite value 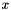 such that there is no other finite value
such that there is no other finite value 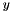 where
where 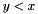 .
.
- Note
- This is different from
OFnumeric_limits<T>::min()for floating-point types.
C++11 standard definitions used:
| T | lowest() |
|---|---|
| non-specialized | T() |
| OFBool | OFFalse |
| char | CHAR_MIN |
| signed char | SCHAR_MIN |
| unsigned char | 0 |
| signed short | SHRT_MIN |
| unsigned short | 0 |
| signed int | INT_MIN |
| unsigned int | 0 |
| signed long | LONG_MIN |
| unsigned long | 0 |
| float | -FLT_MAX |
| double | -DBL_MAX |
◆ max()
|
static |
The maximum finite value representable by the numeric type T.
- Note
- Meaningful for all bounded types.
C++11 standard definitions used:
| T | max() |
|---|---|
| non-specialized | T() |
| OFBool | OFTrue |
| char | CHAR_MAX |
| signed char | SCHAR_MAX |
| unsigned char | UCHAR_MAX |
| signed short | SHRT_MAX |
| unsigned short | USHRT_MAX |
| signed int | INT_MAN |
| unsigned int | UINT_MAX |
| signed long | LONG_MAX |
| unsigned long | ULONG_MAX |
| float | FLT_MAX |
| double | DBL_MAX |
◆ min()
|
static |
The minimum finite value representable by the numeric type T.
For floating-point types with denormalization, min returns the minimum positive normalized value.
- Note
- This behavior may be unexpected, especially when compared to the behavior of min for integral types. To find the value that has no values less than it, use
OFnumeric_limits<T>::lowest(). - Min is only meaningful for bounded types and for unbounded unsigned types, that is, types that represent an infinite set of negative values have no meaningful minimum.
C++11 standard definitions used:
| T | min() |
|---|---|
| non-specialized | T() |
| OFBool | OFFalse |
| char | CHAR_MIN |
| signed char | SCHAR_MIN |
| unsigned char | 0 |
| signed short | SHRT_MIN |
| unsigned short | 0 |
| signed int | INT_MIN |
| unsigned int | 0 |
| signed long | LONG_MIN |
| unsigned long | 0 |
| float | FLT_MIN |
| double | DBL_MIN |
◆ quiet_NaN()
|
static |
The special value quiet not-a-number, as represented by the floating-point type T.
- Note
- Only meaningful if
OFnumeric_limits<T>::has_quiet_NaN == OFTrue. - In IEEE 754, the most common binary representation of floating-point numbers, any value with all bits of the exponent set and at least one bit of the fraction set represents a NaN. It is implementation-defined which values of the fraction represent quiet or signaling NaNs, and whether the sign bit is meaningful.
C++11 standard definitions used:
| T | quiet_NaN() |
|---|---|
| non-specialized | T() |
| OFBool | OFFalse |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | NAN or platform / compiler specific |
| double | platform / compiler specific |
◆ round_error()
|
static |
The largest possible rounding error in ULPs (units in the last place) as defined by ISO 10967, which can vary from 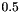 (rounding to the nearest digit) to
(rounding to the nearest digit) to 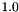 (rounding to zero or to infinity).
(rounding to zero or to infinity).
- Note
- It is only meaningful if
OFnumeric_limits<T>::is_integer == OFFalse.
C++11 standard definitions used:
| T | round_error() |
|---|---|
| non-specialized | T() |
| OFBool | OFFalse |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | 0.5f |
| double | 0.5 |
◆ signaling_NaN()
|
static |
The special value signaling not-a-number, as represented by the floating-point type T.
- Note
- Only meaningful if
OFnumeric_limits<T>::has_signaling_NaN == OFTrue. - In IEEE 754, the most common binary representation of floating-point numbers, any value with all bits of the exponent set and at least one bit of the fraction set represents a NaN. It is implementation-defined which values of the fraction represent quiet or signaling NaNs, and whether the sign bit is meaningful.
C++11 standard definitions used:
| T | signaling_NaN() |
|---|---|
| non-specialized | T() |
| OFBool | OFFalse |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | platform / compiler specific |
| double | platform / compiler specific |
Member Data Documentation
◆ digits
|
static |
The number of digits in base-radix that can be represented by the type T without change.
For integer types, this is the number of bits not counting the sign bit. For floating-point types, this is the number of digits in the mantissa.
C++11 standard definitions used:
| T | digits |
|---|---|
| non-specialized | 0 |
| OFBool | 1 |
| char | is_signed() ? CHAR_BIT : CHAR_BIT - 1 |
| signed char | CHAR_BIT - 1 |
| unsigned char | CHAR_BIT |
| signed short | CHAR_BIT * sizeof(signed short) - 1 |
| unsigned short | CHAR_BIT * sizeof(unsigned short) |
| signed int | CHAR_BIT * sizeof(signed int) - 1 |
| unsigned int | CHAR_BIT * sizeof(unsigned int) |
| signed long | CHAR_BIT * sizeof(signed long) - 1 |
| unsigned long | CHAR_BIT * sizeof(unsigned long) |
| float | FLT_MANT_DIG |
| double | DBL_MANT_DIG |
◆ digits10
|
static |
The number of base-10 digits that can be represented by the type T without change, that is, any number with this many decimal digits can be converted to a value of type T and back to decimal form, without change due to rounding or overflow.
For base-radix types, it is the value of digits (digits-1 for floating-point types) multiplied by 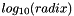 and rounded down.
and rounded down.
C++11 standard definitions used:
| T | digits10 |
|---|---|
| non-specialized | 0 |
| OFBool | 0 |
| char | |
| signed char | |
| unsigned char | |
| signed short | |
| unsigned short | |
| signed int | |
| unsigned int | |
| signed long | |
| unsigned long | |
| float | FLT_DIG |
| double | DBL_DIG |
◆ has_denorm
|
static |
Identifies the floating-point types that support subnormal values.
C++11 standard definitions used:
| T | has_denorm |
|---|---|
| non-specialized | OFdenorm_absent |
| OFBool | OFdenorm_absent |
| char | OFdenorm_absent |
| signed char | OFdenorm_absent |
| unsigned char | OFdenorm_absent |
| signed short | OFdenorm_absent |
| unsigned short | OFdenorm_absent |
| signed int | OFdenorm_absent |
| unsigned int | OFdenorm_absent |
| signed long | OFdenorm_absent |
| unsigned long | OFdenorm_absent |
| float | usually OFdenorm_present |
| double | usually OFdenorm_present |
◆ has_denorm_loss
|
static |
OFTrue for all floating-point types T capable of distinguishing loss of precision due to denormalization from other causes of inexact result.
- Note
- Standard-compliant IEEE 754 floating-point implementations may detect the floating-point underflow at three predefined moments:
- after computation of a result with absolute value smaller than
OFnumeric_limits<T>::min(), such implementation detects tinyness before rounding. - after rounding of the result to
OFnumeric_limits<T>::digitsbits, if the result is tiny, such implementation detects tinyness after rounding. - if the conversion of the rounded tiny result to subnormal form resulted in the loss of precision, such implementation detects denorm loss.
- after computation of a result with absolute value smaller than
C++11 standard definitions used:
| T | has_denorm_loss |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFFalse |
| char | OFFalse |
| signed char | OFFalse |
| unsigned char | OFFalse |
| signed short | OFFalse |
| unsigned short | OFFalse |
| signed int | OFFalse |
| unsigned int | OFFalse |
| signed long | OFFalse |
| unsigned long | OFFalse |
| float | platform / compiler specific |
| double | platform / compiler specific |
◆ has_infinity
|
static |
OFTrue for all types T capable of representing the positive infinity as a distinct special value.
- Note
- This constant is meaningful for all floating-point types and is guaranteed to be
OFTrueifOFnumeric_limits<T>::is_iec559 == OFTrue.
C++11 standard definitions used:
| T | has_infinity |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFFalse |
| char | OFFalse |
| signed char | OFFalse |
| unsigned char | OFFalse |
| signed short | OFFalse |
| unsigned short | OFFalse |
| signed int | OFFalse |
| unsigned int | OFFalse |
| signed long | OFFalse |
| unsigned long | OFFalse |
| float | usually OFTrue |
| double | usually OFTrue |
◆ has_quiet_NaN
|
static |
OFTrue for all types T capable of representing the special value Quiet Not-A-Number.
- Note
- This constant is meaningful for all floating-point types and is guaranteed to be
OFTrueifOFnumeric_limits<T>::is_iec559 == OFTrue.
C++11 standard definitions used:
| T | has_quit_NaN |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFFalse |
| char | OFFalse |
| signed char | OFFalse |
| unsigned char | OFFalse |
| signed short | OFFalse |
| unsigned short | OFFalse |
| signed int | OFFalse |
| unsigned int | OFFalse |
| signed long | OFFalse |
| unsigned long | OFFalse |
| float | usually OFTrue |
| double | usually OFTrue |
◆ has_signaling_NaN
|
static |
OFTrue for all types T capable of representing the special value Signaling Not-A-Number.
- Note
- This constant is meaningful for all floating-point types and is guaranteed to be
OFTrueifOFnumeric_limits<T>::is_iec559 == OFTrue.
C++11 standard definitions used:
| T | has_signaling_NaN |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFFalse |
| char | OFFalse |
| signed char | OFFalse |
| unsigned char | OFFalse |
| signed short | OFFalse |
| unsigned short | OFFalse |
| signed int | OFFalse |
| unsigned int | OFFalse |
| signed long | OFFalse |
| unsigned long | OFFalse |
| float | usually OFTrue |
| double | usually OFTrue |
◆ is_bounded
|
static |
OFTrue for all arithmetic types T that represent a finite set of values.
- Note
- While all fundamental types are bounded, this constant would be
OFFalsein a specialization ofOFnumeric_limitsfor a library-provided arbitrary precision arithmetic type.
C++11 standard definitions used:
| T | is_bounded |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFTrue |
| char | OFTrue |
| signed char | OFTrue |
| unsigned char | OFTrue |
| signed short | OFTrue |
| unsigned short | OFTrue |
| signed int | OFTrue |
| unsigned int | OFTrue |
| signed long | OFTrue |
| unsigned long | OFTrue |
| float | OFTrue |
| double | OFTrue |
◆ is_exact
|
static |
OFTrue for all arithmetic types T that use exact representation.
- Note
- While all fundamental types T for which
OFnumeric_limits<T>::is_exact == OFTrueare integer types, a library may define exact types that aren't integers, e.g. a rational arithmetics type representing fractions.
C++11 standard definitions used:
| T | is_exact |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFTrue |
| char | OFTrue |
| signed char | OFTrue |
| unsigned char | OFTrue |
| signed short | OFTrue |
| unsigned short | OFTrue |
| signed int | OFTrue |
| unsigned int | OFTrue |
| signed long | OFTrue |
| unsigned long | OFTrue |
| float | OFFalse |
| double | OFFalse |
◆ is_iec559
|
static |
OFTrue for all floating-point types T which fulfill the requirements of IEC 559 (IEEE 754) standard.
- Note
- If
OFnumeric_limits<T>::is_iec559 == OFTrue, thenOFnumeric_limits<T>::has_infinity,OFnumeric_limits<T>::has_quiet_NaN, andOFnumeric_limits<T>::has_signaling_NaNare alsoOFTrue.
C++11 standard definitions used:
| T | is_iec559 |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFFalse |
| char | OFFalse |
| signed char | OFFalse |
| unsigned char | OFFalse |
| signed short | OFFalse |
| unsigned short | OFFalse |
| signed int | OFFalse |
| unsigned int | OFFalse |
| signed long | OFFalse |
| unsigned long | OFFalse |
| float | usually OFTrue |
| double | usually OFTrue |
◆ is_integer
|
static |
OFTrue for all integer arithmetic types T and OFFalse otherwise.
C++11 standard definitions used:
| T | is_integer |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFTrue |
| char | OFTrue |
| signed char | OFTrue |
| unsigned char | OFTrue |
| signed short | OFTrue |
| unsigned short | OFTrue |
| signed int | OFTrue |
| unsigned int | OFTrue |
| signed long | OFTrue |
| unsigned long | OFTrue |
| float | OFFalse |
| double | OFFalse |
◆ is_modulo
|
static |
OFTrue for all arithmetic types T that handle overflows with modulo arithmetic, that is, if the result of addition, subtraction, multiplication, or division of this type would fall outside the range ![$[min(), max()]$](form_0.png) , the value returned by such operation differs from the expected value by a multiple of
, the value returned by such operation differs from the expected value by a multiple of 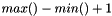 .
.
C++11 standard definitions used:
| T | is_modulo |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFFalse |
| char | platform / compiler specific |
| signed char | platform / compiler specific |
| unsigned char | OFTrue |
| signed short | platform / compiler specific |
| unsigned short | OFTrue |
| signed int | platform / compiler specific |
| unsigned int | OFTrue |
| signed long | platform / compiler specific |
| unsigned long | OFTrue |
| float | OFFalse |
| double | OFFalse |
◆ is_signed
|
static |
OFTrue for all signed arithmetic types T and OFFalse for the unsigned types.
C++11 standard definitions used:
| T | is_signed |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFFalse |
| char | platform / compiler specific |
| signed char | OFTrue |
| unsigned char | OFFalse |
| signed short | OFTrue |
| unsigned short | OFFalse |
| signed int | OFTrue |
| unsigned int | OFFalse |
| signed long | OFTrue |
| unsigned long | OFFalse |
| float | OFTrue |
| double | OFTrue |
◆ is_specialized
|
static |
OFTrue for all T for which there exists a specialization of OFnumeric_limits, OFFalse otherwise.
C++11 standard definitions used:
| T | is_specialized |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFTrue |
| char | OFTrue |
| signed char | OFTrue |
| unsigned char | OFTrue |
| signed short | OFTrue |
| unsigned short | OFTrue |
| signed int | OFTrue |
| unsigned int | OFTrue |
| signed long | OFTrue |
| unsigned long | OFTrue |
| float | OFTrue |
| double | OFTrue |
◆ max_digits10
|
static |
The number of base-10 digits that are necessary to uniquely represent all distinct values of the type T, such as necessary for serialization/deserialization to text.
- Note
- This constant is meaningful for all floating-point types.
C++11 standard definitions used:
| T | max_digits10 |
|---|---|
| non-specialized | 0 |
| OFBool | 0 |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | |
| double | |
◆ max_exponent
|
static |
The largest positive number 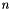 such that
such that 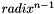 is a valid normalized value of the floating-point type T.
is a valid normalized value of the floating-point type T.
C++11 standard definitions used:
| T | max_exponent |
|---|---|
| non-specialized | 0 |
| OFBool | 0 |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | FLT_MAX_EXP |
| double | DBL_MAX_EXP |
◆ max_exponent10
|
static |
The largest positive number 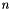 such that
such that 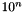 is a valid normalized value of the floating-point type T.
is a valid normalized value of the floating-point type T.
C++11 standard definitions used:
| T | max_exponent10 |
|---|---|
| non-specialized | 0 |
| OFBool | 0 |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | FLT_MAX_10_EXP |
| double | DBL_MAX_10_EXP |
◆ min_exponent
|
static |
The lowest negative number 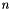 such that
such that 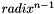 is a valid normalized value of the floating-point type T.
is a valid normalized value of the floating-point type T.
C++11 standard definitions used:
| T | min_exponent |
|---|---|
| non-specialized | 0 |
| OFBool | 0 |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | FLT_MIN_EXP |
| double | DBL_MIN_EXP |
◆ min_exponent10
|
static |
The lowest negative number 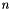 such that
such that 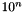 is a valid normalized value of the floating-point type T.
is a valid normalized value of the floating-point type T.
C++11 standard definitions used:
| T | min_exponent10 |
|---|---|
| non-specialized | 0 |
| OFBool | 0 |
| char | 0 |
| signed char | 0 |
| unsigned char | 0 |
| signed short | 0 |
| unsigned short | 0 |
| signed int | 0 |
| unsigned int | 0 |
| signed long | 0 |
| unsigned long | 0 |
| float | FLT_MIN_10_EXP |
| double | DBL_MIN_10_EXP |
◆ radix
|
static |
The base of the number system used in the representation of the type.
It is 2 for all binary numeric types, but it may be, for example, 10 for IEEE 754 decimal floating-point types or for third-party binary-coded decimal integers. This constant is meaningful for all specializations.
C++11 standard definitions used:
| T | radix |
|---|---|
| non-specialized | 0 |
| OFBool | 2 |
| char | 2 |
| signed char | 2 |
| unsigned char | 2 |
| signed short | 2 |
| unsigned short | 2 |
| signed int | 2 |
| unsigned int | 2 |
| signed long | 2 |
| unsigned long | 2 |
| float | FLT_RADIX |
| double | FLT_RADIX |
◆ round_style
|
static |
Identifies the rounding style used by the floating-point type T whenever a value that is not one of the exactly representable values of T is stored in an object of that type.
C++11 standard definitions used:
| T | round_style |
|---|---|
| non-specialized | OFround_toward_zero |
| OFBool | OFround_toward_zero |
| char | OFround_toward_zero |
| signed char | OFround_toward_zero |
| unsigned char | OFround_toward_zero |
| signed short | OFround_toward_zero |
| unsigned short | OFround_toward_zero |
| signed int | OFround_toward_zero |
| unsigned int | OFround_toward_zero |
| signed long | OFround_toward_zero |
| unsigned long | OFround_toward_zero |
| float | usually OFround_to_nearest |
| double | usually OFround_to_nearest |
◆ tinyness_before
|
static |
OFTrue for all floating-point types T that test results of floating-point expressions for underflow before rounding.
- Note
- Standard-compliant IEEE 754 floating-point implementations may detect the floating-point underflow at three predefined moments:
- after computation of a result with absolute value smaller than
OFnumeric_limits<T>::min(), such implementation detects tinyness before rounding. - after rounding of the result to
OFnumeric_limits<T>::digitsbits, if the result is tiny, such implementation detects tinyness after rounding. - if the conversion of the rounded tiny result to subnormal form resulted in the loss of precision, such implementation detects denorm loss.
- after computation of a result with absolute value smaller than
C++11 standard definitions used:
| T | tinyness_before |
|---|---|
| non-specialized | OFFalse |
| OFBool | OFFalse |
| char | OFFalse |
| signed char | OFFalse |
| unsigned char | OFFalse |
| signed short | OFFalse |
| unsigned short | OFFalse |
| signed int | OFFalse |
| unsigned int | OFFalse |
| signed long | OFFalse |
| unsigned long | OFFalse |
| float | platform / compiler specific |
| double | platform / compiler specific |
◆ traps
|
static |
OFTrue for all arithmetic types T that have at least one value that, if used as an argument to an arithmetic operation, will generate a trap.
- Note
- On most platforms integer division by zero always traps, and
OFnumeric_limits<T>::trapsisOFTruefor all integer types that support the value0. The exception is the type OFBool, if support for the native type bool is available: even though division byOFFalsetraps due to integral promotion from OFBool to int, it is the zero-valued int that traps. Zero is not a value of type bool. -
On most platforms, floating-point exceptions may be turned on and off at runtime, in which case the value of
OFnumeric_limits<T>::trapsfor floating-point types reflects the state of floating-point trapping facility at the time of program startup.
C++11 standard definitions used:
| T | traps |
|---|---|
| non-specialized | OFFalse |
| OFBool | usually OFFalse |
| char | usually OFTrue |
| signed char | usually OFTrue |
| unsigned char | usually OFTrue |
| signed short | usually OFTrue |
| unsigned short | usually OFTrue |
| signed int | usually OFTrue |
| unsigned int | usually OFTrue |
| signed long | usually OFTrue |
| unsigned long | usually OFTrue |
| float | usually OFFalse |
| double | usually OFFalse |
The documentation for this struct was generated from the following file:
- ofstd/include/dcmtk/ofstd/oflimits.h